Conjunto

Conjunto vacíoEditar

Artículo principal: Conjunto vacío

El conjunto que no contiene ningún elemento se llama el conjunto vacío y se denota por ∅ o simplemente {}. Algunas teorías axiomáticas de conjuntos aseguran que el conjunto vacío existe incluyendo un axioma del conjunto vacío. En otras teorías, su existencia puede deducirse. Muchas posibles propiedades de conjuntos son trivialmente válidas para el conjunto vacío.

PropiedadesEditar

En la teoría de conjuntos axiomática estándar, por el Axioma de extenionalidad, dos conjuntos son iguales si tienen los mismos elementos; por lo tanto sólo puede haber un conjunto sin ningún elemento. Por consiguiente, sólo hay un único conjunto vacío, y hablamos de "el conjunto vacío" en lugar de "un conjunto vacío".

Para cualquier conjunto A:

(Ver operaciones con conjuntos)

• El conjunto vacío es un subconjunto de A:

  ${\displaystyle \forall A:\emptyset \subseteq A}$

• La unión de A con el conjunto vacío es A:

  ${\displaystyle \forall A:A\cup \emptyset =A}$

• La intersección de A con el conjunto vacío es el conjunto vacío:

  ${\displaystyle \forall A:A\cap \emptyset =\emptyset }$

• El producto cartesiano de A y el conjunto vacío es el conjunto vacío:

  ${\displaystyle \forall A:A\times \emptyset =\emptyset }$

El conjunto vacío tiene las siguientes propiedades:

• Su único subconjunto es el propio conjunto vacío:

  ${\displaystyle \forall A:A\subseteq \emptyset \Rightarrow A=\emptyset }$

• El "conjunto de poder" del conjunto vacío es el conjunto que contiene únicamente el conjunto vacío:

  ${\displaystyle 2^{\emptyset }=\{\emptyset \}}$

• Su número de elementos (cardinalidad) es cero:

  ${\displaystyle \mathrm {card} (\emptyset )=0}$

(La lista de símbolos matemáticos empleados se encuentra aquí).

SubconjuntosEditar

Artículo principal: Subconjunto

Subconjunto. B es un subconjunto de A (en particular un subconjunto propio).

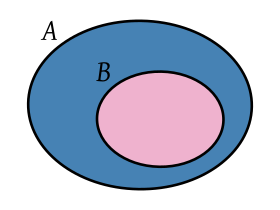
Un subconjunto A de un conjunto B, es un conjunto que contiene algunos de los elementos de B (o quizá todos):

Un conjunto A es un subconjunto del conjunto B si cada elemento de A es a su vez un elemento de B.

Cuando A es un subconjunto de B, se denota como A ⊆ B y se dice que «A está contenido en B». También puede escribirse B ⊇ A, y decirse que B es un superconjunto de A y también «B contiene a A» o «B incluye a A».

Todo conjunto A es un subconjunto de sí mismo, ya que siempre se cumple que «cada elemento de A es a su vez un elemento de A». Es habitual establecer una distinción más fina mediante el concepto de subconjunto propio: A es un subconjunto propio de B si es un subconjunto de B pero no es igual a B. Se denota como A ⊊ B, es decir: A ⊆ B pero A ≠ B (y equivalentemente, para un superconjunto propio, B ⊋ A).^{[n 2]}

Ejemplos.

El «conjunto de todos los hombres» es un subconjunto propio del «conjunto de todas las personas».

{1, 3} ⊊ {1, 2, 3, 4}

{1, 2, 3, 4} ⊆ {1, 2, 3, 4}